堆是平衡二叉树数据结构的一种特殊情况,其中根节点密钥与其子节点进行比较并相应地进行排列.如果有子节点,那么 :
key(α) ≥ key(β)
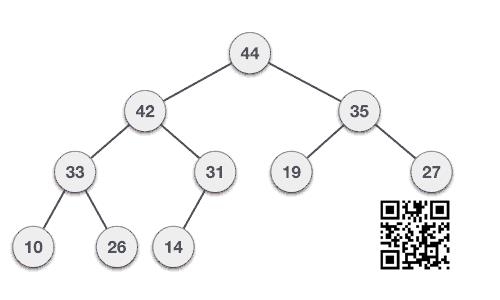
由于parent的值大于child的值,因此该属性生成 Max Heap .基于此标准,堆可以是两种类型 :
For Input → 35 33 42 10 14 19 27 44 26 31
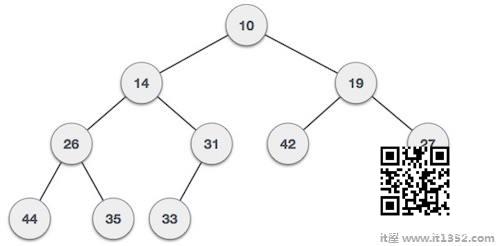
Min-Heap : 根节点的值小于或等于其子节点的值.
Max-Heap : 根节点的值大于或等于其子节点的值.
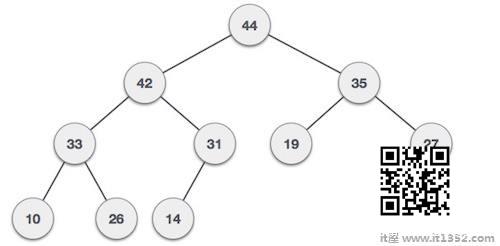
两棵树都使用相同的输入和到达顺序构建.
最大堆构造算法
我们将使用相同的示例来演示如何创建Max Heap.创建Min Heap的过程类似,但是我们使用min值而不是max值.
我们将通过一次插入一个元素来导出最大堆的算法.在任何时候,堆必须保持其属性.在插入时,我们还假设我们在已经堆积的树中插入节点.
步骤1 : 在堆的末尾创建一个新节点. 第2步 : 为节点分配新值. 第3步 : 将此子节点的值与其父节点进行比较. 第4步 : 如果parent的值小于child,则交换它们. 第5步 : 重复步骤3& 4直到Heap属性成立.
注意 : 在Min Heap构造算法中,我们期望父节点的值小于子节点的值.
让我们通过动画插图来理解Max Heap的构造.我们考虑前面使用的相同输入样本.

最大堆删除算法
让我们派生一个从最大堆中删除的算法. Max(或Min)堆中的删除总是在根处发生,以删除最大(或最小)值.
步骤1 : 删除根节点. 第2步 : 将最后一级的最后一个元素移动到root. 第3步 : 将此子节点的值与其父节点进行比较. 第4步 : 如果parent的值小于child,则交换它们. 第5步 : 重复步骤3& 4直到Heap属性成立.