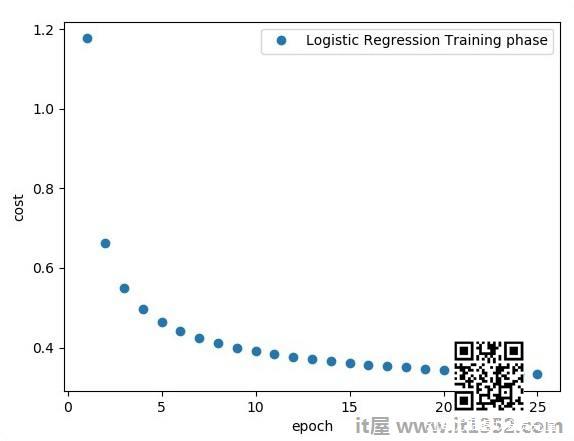
为了理解单层感知器,理解人工神经网络(ANN)非常重要.人工神经网络是信息处理系统,其机制受到生物神经回路功能的启发.人工神经网络拥有许多彼此连接的处理单元.以下是人工神经网络的示意图 :
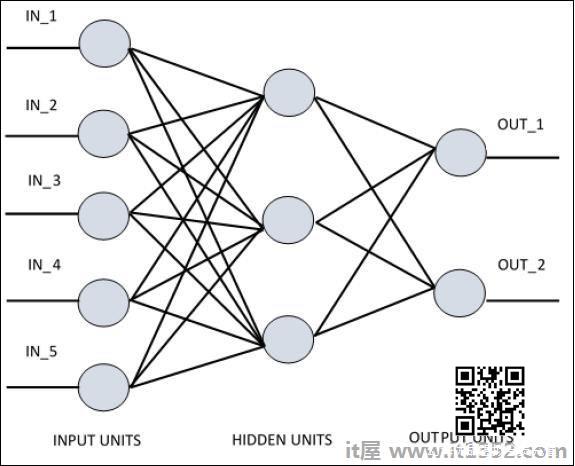
该图显示隐藏单元与外部层通信.而输入和输出单元仅通过网络的隐藏层进行通信.
与节点的连接模式,层的总数和输入与输出之间的节点级别与数量每层神经元定义神经网络的架构.
有两种类型的架构.这些类型关注功能人工神经网络,如下所示;
单层感知器
多层感知器
单层感知器
单层感知器是第一个提出的神经模型.神经元的局部记忆的内容由权重向量组成.单层感知器的计算是在输入矢量的和的计算中执行的,每个输入矢量的值乘以权重的矢量的相应元素.输出中显示的值将是激活函数的输入.
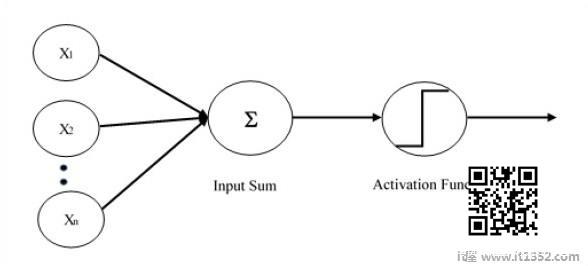
让我们专注于使用TensorFlow实现图像分类问题的单层感知器.说明单层感知器的最好例子是通过"Logistic回归"的表示.
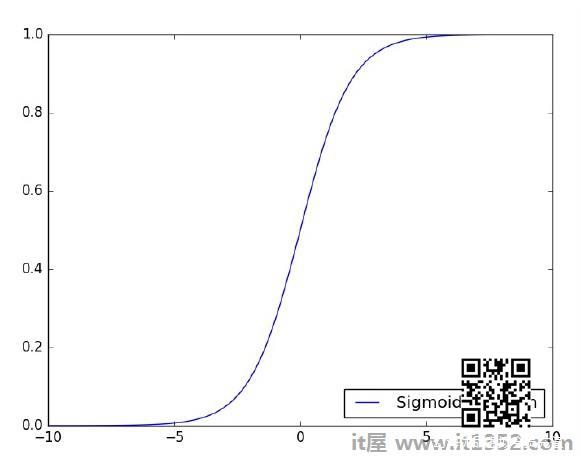
现在,让我们考虑以下基本步骤来训练逻辑回归 :
在训练开始时使用随机值初始化权重.
对于训练集的每个元素,计算误差与期望输出和实际输出.计算的误差用于调整权重.
重复该过程,直到整个训练集上的错误不小于指定的阈值,直到达到了最大迭代次数.
下面提到评估逻辑回归的完整代码 :
# Import MINST data from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("/tmp/data/", one_hot = True) import tensorflow as tf import matplotlib.pyplot as plt # Parameters learning_rate = 0.01 training_epochs = 25 batch_size = 100 display_step = 1 # tf Graph Input x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784 y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes # Create model # Set model weights W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10])) # Construct model activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax # Minimize error using cross entropy cross_entropy = y*tf.log(activation) cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1)) optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost) #Plot settings avg_set = [] epoch_set = [] # Initializing the variables init = tf.initialize_all_variables()# Launch the graph with tf.Session() as sess: sess.run(init) # Training cycle for epoch in range(training_epochs): avg_cost = 0. total_batch = int(mnist.train.num_examples/batch_size) # Loop over all batches for i in range(total_batch): batch_xs, batch_ys = \ mnist.train.next_batch(batch_size) # Fit training using batch data sess.run(optimizer, \ feed_dict = { x: batch_xs, y: batch_ys}) # Compute average loss avg_cost += sess.run(cost, \ feed_dict = { x: batch_xs, \ y: batch_ys})/total_batch # Display logs per epoch step if epoch % display_step == 0: print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost)) avg_set.append(avg_cost) epoch_set.append(epoch+1) print ("Training phase finished") plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase') plt.ylabel('cost') plt.xlabel('epoch') plt.legend() plt.show() # Test model correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1)) # Calculate accuracy accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print ("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))输出
以上代码生成以下输出 :
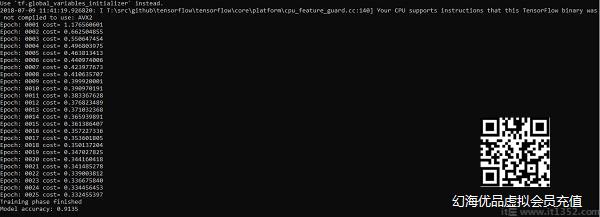
逻辑回归被视为预测分析. Logistic回归用于描述数据并解释一个从属二元变量与一个或多个名义或自变量之间的关系.